‒ ¿Qué son los números enteros?
Los números naturales aparecieron o se crearon, por la necesidad del hombre de contar o de saber lo que poseía, y los números enteros se crearon, para poder expresar cosas que faltan o no se poseen como una deuda financiera.
Con los números naturales se pueden hacer sumas y multiplicaciones, pero no todos los números naturales se pueden usar para hacer restas o divisiones. El echo de que con los números naturales no podamos hacer una resta, cuando el minuendo es mayor que el sustraendo, obligo también al hombre a crear el conjunto de los número enteros. Otro motivo de la creación de los números enteros, esta en que existen muchas situaciones en la que los números naturales no nos permiten representar ciertas cantidades, como por ejemplo la temperatura bajo cero, y la profundidad a la que se sumerge un submarino con respecto al nivel del mar, etc. Veamos dos ejemplos, en donde el primero tiene solución con números naturales y el segundo no.
Ejemplo 1.
Jorge invirtió S/ 10 000 PEN en un negocio, pero a fin de mes gasto S/ 5 000 PEN. ¿Cuánto dinero le queda?
10 000 – 5 000 = 5 000
En este ejemplo se puede observar que podemos hacer una resta, ya que la cantidad de dinero que se gasto, representa el número que tiene que quitarle a 10 000, para obtener los 5000, que es el dinero que le queda.
Ejemplo 2.
Jorge invirtió S/ 10 000 PEN en un negocio, pero a fin de mes gasto S/ 15 000 PEN. ¿Cuánto dinero le queda?
10 000 – 15 000 = ?
En esta situación se puede observar que no podemos hacer una resta, ya que la cantidad de dinero que se gasto y que representa el número que tiene que quitarle a 10 000 es mayor. No obstante podemos restar los números al revés, es decir 15 000 – 10 000, que nos da 5000, pero esa cantidad en si no representa lo que le queda, si no que más bien representa la cantidad de dinero que debe o que posiblemente pidio prestado para poder continuar con su negocio. Cantidades así no podemos representarlas con los números naturales, ya que esa cantidad en sí es algo que jorge no tiene y no lo puede contar.
Para dar solución a estos problemas necesitamos de los números enteros. Pero antes debemos conocer lo que son los números negativos y positivos, un número negativo es cualquier número menor que 0, y un número positivo es cualquier número mayor que 0. De esto también podemos deducir que los números naturales están compuestos del 0 y los números positivos.
Un número negativo se representa con un signo – delante del número, y un número positivo se representa con un signo + delante del número, aunque en el caso de los números positivos no es necesario usar el signo +, a menos que se requiera.
El conjunto de los números negativos se expresan del siguiente modo:
ℤ-={x/x, x<0}
en donde x es cualquier número negativo y este es menor que 0, y los números positivos se expresan del siguiente modo:
ℤ+={x/x, x>0}
En donde x es cualquier número positivo y mayor que cero.
Ejemplo 3.
Escribir los siguientes números.
Enunciado número -3 +4 o 4 -5 +12 o 12 +4000 o 4000 -2000 S/. - 300 PEN
Los números negativos, el 0 y los números positivos, formarán lo que se conoce como el conjunto de los números enteros. Los números enteros se suelen representar de la siguiente manera:
ℤ={-∞, ..., -11, -10, -9, -8, -7, -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, ..., ∞}
El símbolo ℤ se usa para representar a los números enteros, y ℤ+ para los números positivos y ℤ- para los negativos. al igual que los números naturales estos son infinitos, pero son infinitos positivos ∞ e infinitos negativos -∞.
Ahora que ya se explico sobre los número negativos podemos solucionar el problema del ejemplo 2.
Ejemplo 4.
Jorge invirtió S/ 10 000 PEN en un negocio, pero a fin de mes gasto S/ 15 000 PEN. ¿Cuánto dinero le queda?
10 000 – 15 000 = ?
Obviamente no podemos restar 10 000 de 15 000, pero podemos hacerlo al revés es decir restamos 15 000 de 10 000, y obtendremos 5000. Y como estos cinco mil representa una deuda, y es algo que jorge no tiene y por ende no puede contarlo, entonces es algo que no podemos representar con los números naturales, para lo cual debemos usar los números negativos y representar los 5000 como -5000. Que si representa algo que no tiene Jorge, y que es la cantidad de dinero que ahora debe Jorge. Y la respuesta a este problema es que a Jorge, no le quedo nada y que él debe o tiene una deuda pendiente de S/ -5000 PEN.
‒ Representación gráfica de los números enteros.
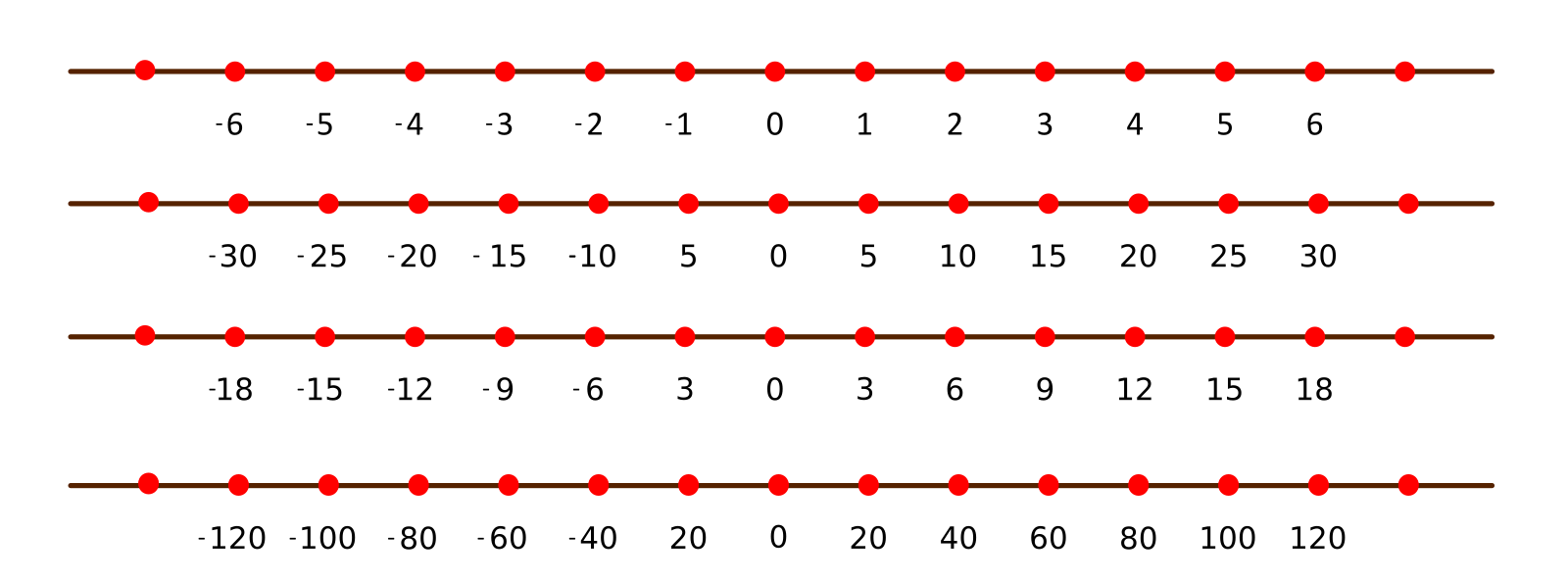
Al igual que los números naturales estos también se pueden representar sobre una recta.
Cuando se representan los números enteros sobre una recta, esta puede ser graduada de varias maneras: de 1 en 1, de 2 en 2, de 20 en 20 etc. La distancia entre dos puntos de la recta debe ser siempre la misma. A continuación unos ejemplos:
Última revisión: 26/08/2017.